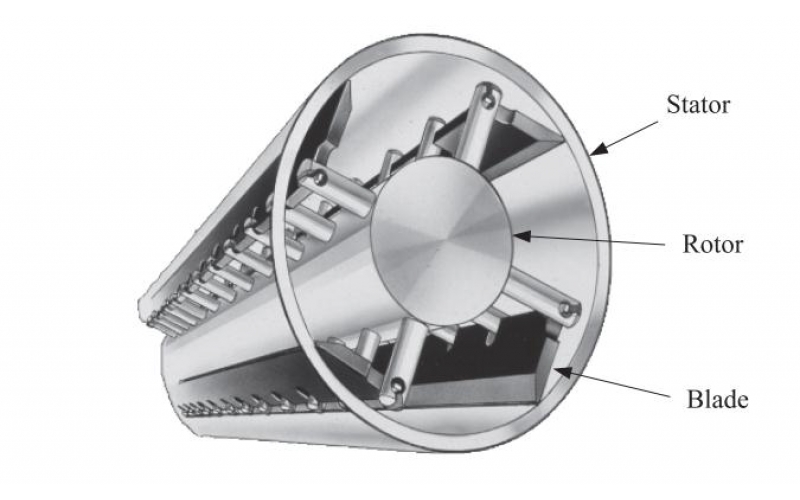
Je uveden jednoduchý matematický model proudění tekutiny v běžném typu výměníku tepla se škrabaným povrchem, ve kterém jsou mezery mezi lopatkami a stěnami zařízení úzké, takže je platný popis proudění z teorie mazání.Konkrétně se analyzuje ustálené izotermické proudění newtonské tekutiny kolem periodického pole otočných stíracích lopatek v kanálu s jednou pevnou a jednou pohyblivou stěnou, když je aplikován tlakový gradient ve směru kolmém na pohyb stěny.Proudění je trojrozměrné, ale přirozeně se rozkládá na dvourozměrné „příčné“ proudění poháněné hraničním pohybem a „podélné“ proudění řízené tlakem.Jsou odvozeny první detaily struktury příčného proudění a zejména jsou vypočteny rovnovážné polohy lopatek.Je ukázáno, že požadovaného kontaktu mezi lopatkami a pohyblivou stěnou bude dosaženo za předpokladu, že lopatky budou natočeny dostatečně blízko jejich konců.Když je dosaženo požadovaného kontaktu, model předpovídá, že síly a krouticí momenty na lopatkách jsou singulární, a tak je model zobecněn tak, aby zahrnoval tři další fyzikální efekty, jmenovitě chování nenewtonského mocninného zákona, prokluzování na pevných hranicích a kavitaci. v oblastech velmi nízkého tlaku, z nichž každá je ukázána k vyřešení těchto singularit.Nakonec je diskutována povaha podélného proudění.
Čas odeslání: 22. června 2021